1272:铺瓷砖-2
时间限制:2 S / 内存限制:65536 KB
AC:110 / Submit:171
| 问题描述 |
|---|
对于一个$$3$$行$$m$$列的走道。 现在用$$1*3、2*3、3*3$$的砖去铺满,一共有多少种不同的铺法? 瓷砖可以旋转:即$$1*3$$的砖可以旋转成$$3*1$$,同理$$2*3$$可以旋转成$$3*2$$。 以下是一个$$3$$行$$10$$列的一种铺法: 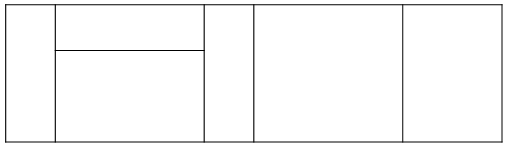 |
| 输入描述 |
第一行是一个正整数$$n$$,表示测试案例的数量。 每组测试案例中,有一个正整数$$m$$,表示走道是$$m$$列的。($$1 \le m \le 100$$) |
| 输出描述 |
针对每组案例,输出一个数字,表示不同的铺法的数量,保证答案不会超过$$10^{100}$$。 |
| 样例输入复制样例 |
3 1 3 50 |
| 样例输出 |
1 7 177822624501049026 |
| 相关 |