1910:过桥问题-2
时间限制:2 S / 内存限制:65536 KB
AC:13 / Submit:24
| 问题描述 |
|---|
某物流公司准备驶出$$K$$辆货车从甲地开往丙地。
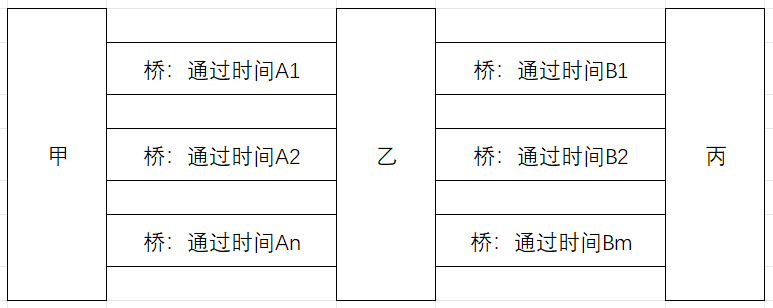
如上图所示,货车在行驶的过程中需要先过桥到达乙地后再过桥到达目的地丙。 令人担忧的是,每座桥的最大限重都不足以同时承受两辆货车的重量,这意味着同一时间一座桥只能过一部车。 每一座桥由于交通情况,通过的时间也不见得相同。 连接甲乙两地共有$$N$$座桥,通过时间分别为$$A_1-A_N$$。 连接乙丙两地共有$$M$$座桥,通过时间分别为$$B_1-B_M$$。 每一辆货车在甲地和乙地都可以选择停留,等待某一座桥的货车通过后再驶出;当然也可以选择一座没有货车的桥直接驶出。 请你确认$$K$$辆货车从甲地开往丙地的最小时间。 |
| 输入描述 |
第一行三个正整数$$K,N,M$$含义如描述。($$1 \leq K,N,M \leq 10^5$$) 第二行$$N$$个整数分别表示$$A_1-A_N$$。($$1 \leq A_i \leq 10^9$$) 第三行$$M$$个整数分别表示$$B_1-B_M$$。($$1 \leq B_i \leq 10^9$$) |
| 输出描述 |
在一行中输出$$K$$辆货车从甲地开往丙地的最小时间。 |
| 样例输入复制样例 |
2 2 3 10 100 15 12 20 |
| 样例输出 |
32 |
| 提示说明 |
第一辆车选择通过时间为$$10$$的桥到达乙,紧接着,选择通过时间为$$15$$的桥到达丙,总用时$$25$$。 第二辆车在第一辆车到达乙的同时,开始从通过时间为$$10$$的桥出发,到达后选择通过时间为$$12$$的桥到达丙。 总用时为:$$10+10+12=32$$,其中第一个$$10$$为等待第一辆车的时间,可以发现这种方案是最快的。 |
| 相关 |