2556:新能源车
时间限制:2 S / 内存限制:65536 KB
AC:12 / Submit:36
| 问题描述 |
|---|
罗少过年开着自家的新能源车打算来一次痛快的城市旅行。 已知罗少所在地区可以看成由$$n$$个点$$m$$条边构成的无向图。(点代表城市,边代表道路) 罗少每行驶$$1$$单位距离,车就会损耗$$1$$的电量。 由于充电是一件很麻烦的事,因此罗少希望在旅行的过程中尽可能少的充电。 充电桩只可能出现在城市中,罗少每到一个城市都有两种选择:要么不充电,要么把电充满。 罗少在出发前想知道,从一个城市$$x$$满电出发的情况下到达城市$$y$$至少需要充多少次电。 |
| 输入描述 |
第一行是三个正整数$$n,m,L$$分别表示点的数量,边的数量以及电池的最大容量。($$1 \leq n \leq 300、1 \leq L \leq 10^9$$) 接下来$$m$$行,每行三个正整数$$a,b,c$$表示城市$$a$$和城市$$b$$之间有一条距离为$$c$$的路。($$1 \leq a,b \leq n、1 \leq c \leq 10^9$$,保证没有重边和自环,因此不再给出$$m$$的范围) 然后是一个正整数$$T$$表示询问的次数。($$1 \leq T \leq 10^5$$,询问之间是相互独立的) 每次询问包含两个正整数$$x,y$$,表示待查询的城市。($$1 \leq x,y \leq n$$,$$x,y$$可能相同) |
| 输出描述 |
输出$$T$$行,针对每次询问的城市$$x,y$$,回答从城市$$x$$到城市$$y$$至少需要充多少次电,如果无法到达,输出$$-1$$。 |
| 样例输入复制样例 |
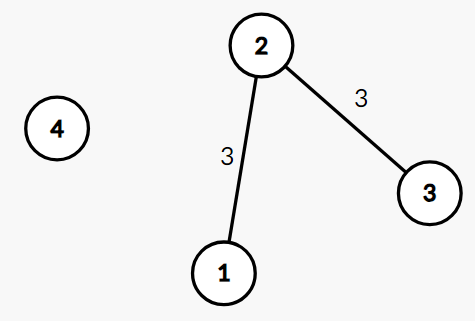
4 2 5 1 2 3 2 3 3 3 3 2 1 3 2 4 |
| 样例输出 |
0 1 -1 |
| 提示说明 |
|
| 相关 |