2636:多汁牧场(Hard)
时间限制:2 S / 内存限制:65536 KB
AC:23 / Submit:102
| 问题描述 |
|---|
有一片草原,我们可以把它看成一张$$n \times m$$的网格图。 这片草原由草地和树木组成,牧民们打算划出一块矩形的区域用于放牧。 经过实地考察,牧民们发现树木容易阻挡视线,故划出的部分不能包含树木。 已知这片草原上$$p$$棵树的位置,你的任务是,确定牧民们最大可以划出的放牧区域面积。 |
| 输入描述 |
第一行是一个正整数$$T$$表示测试案例的数量。($$1 \leq T \leq \red{1000}$$) 每组案例先是两个正整数$$n,m$$表示草原的行数和列数。($$1 \leq n,m \leq \red{10^9}$$) 接下来一个正整数$$p$$表示树木的数量,保证所有树木的位置互不相同。($$1 \leq p \leq \red{1000}$$) 然后$$p$$行,每行两个正整数$$x,y$$表示草原的第$$x$$行第$$y$$列是树木。($$1 \leq x \leq n,1 \leq y \leq m$$) 保证$$T$$组案例的$$p$$之和不会超过$$\red{1000}$$,Easy 和 Hard 版本的区别仅在于数据规模(已用红色字体标出)。 |
| 输出描述 |
在一行中输出放牧区域面积的最大值。 |
| 样例输入复制样例 |
1 5 5 2 1 1 3 4 |
| 样例输出 |
12 |
| 提示说明 |
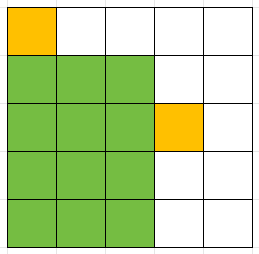
橙色表示树木,绿色表示放牧区域。
|
| 相关 |