2735:陀螺区域的最大值
时间限制:2 S / 内存限制:65536 KB
AC:11 / Submit:15
| 问题描述 |
|---|
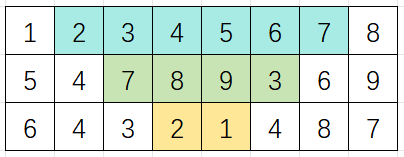
给定一个$$3$$行$$n$$列的长方形网格,请从中找出一片陀螺形状的区域,使得这片区域的分数之和达到最大。 如下图就是一个陀螺形状的区域(但分数并不是最大的)。
形式化的表示,若第一行选中区域的左右端点分别为$$a,b$$,第二行为$$c,d$$第三行为$$e,f$$,那么有$$1 \le a \lt c \lt e \le f \lt d \lt b \le n$$。 |
| 输入描述 |
第一行是一个正整数$$n$$表示长方形区域的列数。($$5 \le n \le 10^5$$) 接下来输入$$3$$行$$n$$列个$$[-2000,2000]$$之间的整数分别表示长方形网格中的数字。 |
| 输出描述 |
在一行中输出陀螺区域的最大值。 |
| 样例输入复制样例 |
8 -1 2 3 -4 5 6 -7 8 5 4 -7 8 9 -3 6 -9 6 -4 3 2 -1 4 -8 7 |
| 样例输出 |
37 |
| 相关 |