3234:搭桥
时间限制:2 S / 内存限制:65536 KB
AC:79 / Submit:127
| 问题描述 |
|---|
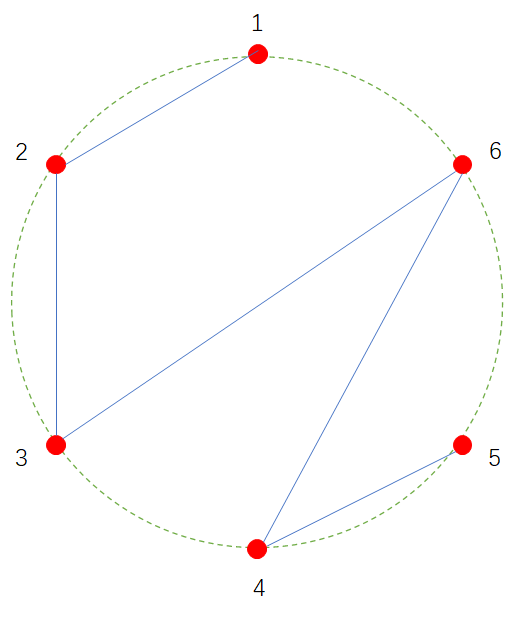
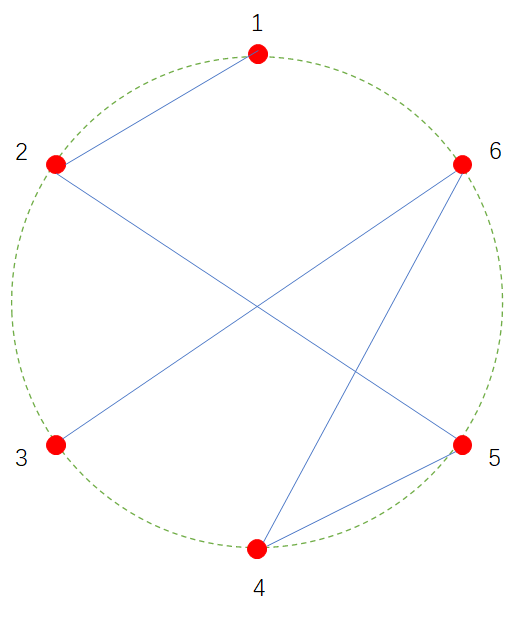
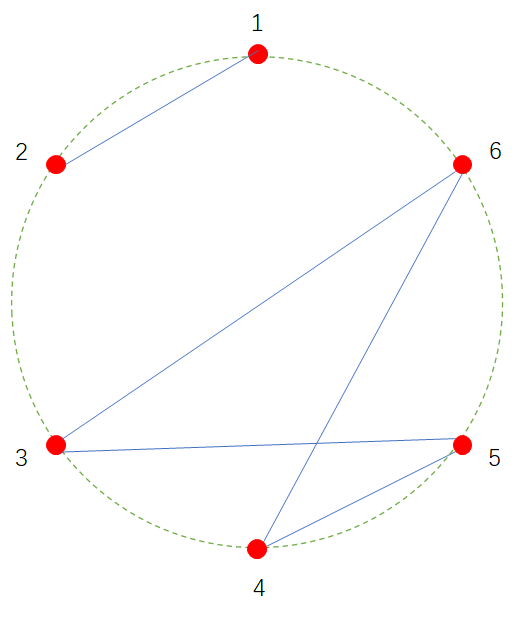
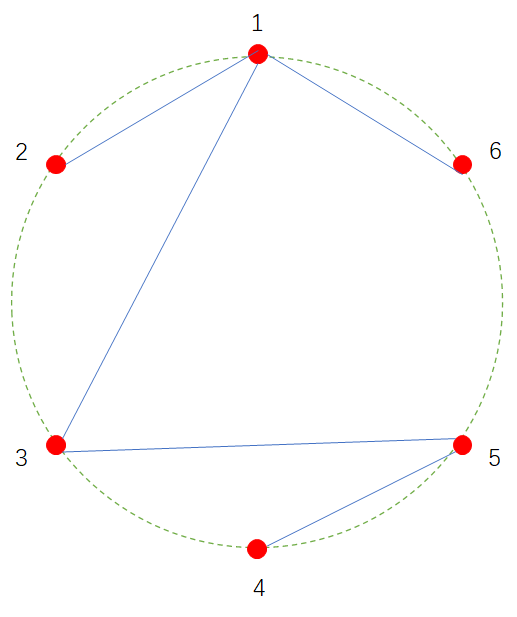
在一片海域上散布着m个岛屿,每个岛屿上有一座村庄,岛屿的位置恰好处在正m边形的顶点上。为了让居民能够不需要坐船就能到达任意一个村庄,村长们决定在村庄之间修桥,修桥按照以下四个原则: 1、总共修m-1座桥,每座桥用于直线连接两座村庄,不经过第三座村庄; 2、任意两个岛屿的村民都可以通过经过若干桥梁碰面; 3、每两个岛屿之间最多修1座桥,每个岛屿最多只能与2座桥相连接; 4、任意两座桥不得在空间上相交错,也就是说,把桥梁当作线段,任意两个线段都不能在非线段顶点处有交点。 已知村庄的数量m,求有多少种不同的岛屿间桥梁的连接方法。由于这个值可能非常大,故只要输出该值对100000007取模(取余数)的结果。 下图中图1是一种合法的桥梁修建方法;图2不合法,因为2-5和3-6、4-6桥梁之间有交错;图3不合法,因为1、2和3、4、5、6之间不连通;图4不合法,因为1号岛屿与3座桥相连接。
|
| 输入描述 |
多组案例。一个正整数n,表示案例的数量。(n <= 20) 每组案例由一个正整数m组成,表示岛屿的数量。(2 <= m <= 1e8) |
| 输出描述 |
针对每组案例,输出一个整数,表示桥梁连接方法的数量对100000007取模的结果。 每组案例输出完都要换行。 |
| 样例输入复制样例 |
4 2 3 6 100000000 |
| 样例输出 |
1 3 48 50195316 |
| 提示说明 |
当m=3时,有3种不同的连接方法:1-2-3、2-1-3、1-3-2,注意1-2-3和3-2-1是同一种连接方法,都是1、2之间盖一座桥,2、3之间盖一座桥,不要重复统计。 |
| 相关 |