3410:飞行棋
时间限制:1 S / 内存限制:65536 KB
AC:46 / Submit:155
| 问题描述 |
|---|
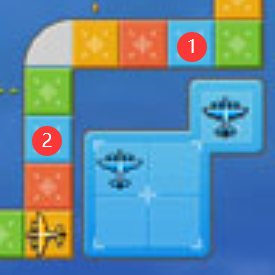
在飞行棋中,有一条规则是:在本次飞行完毕后,若落点格子的颜色与飞机的颜色相同则可以跳跃到下一个颜色相同的格子。
如上图,若蓝色玩家骰出 2 点,那么它可以飞到①号格子中,由于①号格子与飞机颜色都是蓝色,所以可以直接跳跃到②号格中。 现在假设飞行棋棋盘是一个有 n 个格子的环,按顺序分别编号为 1 ~ n,我们用数字来表示格子的颜色,相同的数字即为相同的颜色。 罗少觉得骰子只有 6 面不过瘾,所以他用电脑写了一个随机数生成器来决定他每次飞行的格子数; 同时他觉得只有飞机颜色和落点格子颜色相同时才能跳跃玩的不够尽兴,所以每一次罗少飞行完毕后总是可以跳跃到下一个与当前落点颜色相同的格子。 现在罗少从编号为 1 的格子出发,总共生成了 m 个数字,请问在 m 次飞行结束后,罗少所在的格子编号是多少。 注意:由于棋盘是一个环,所以 n 号格子的下一个就是 1 号格子。 |
| 输入描述 |
第一行是一个正整数 n 表示格子的数量。 然后是 n 个正整数 ci,分别表示 1 ~ n 号格子的颜色。 第三行是一个正整数 m 表示飞行的次数。 然后是 m 个正整数 xi,分别表示每一次飞行的距离。 测试用例1:输入的所有数字均不会超过 100。 测试用例2:所有格子的颜色均相同。 测试用例3:所有格子的颜色均不同。 对于所有测试用例:输入的所有数字均不会超过 2e5。 |
| 输出描述 |
在 m 次飞行结束后,罗少所在的格子编号是多少,然后换行。 |
| 样例输入复制样例 |
5 1 2 3 1 2 3 1 3 1 |
| 样例输出 |
1 |
| 提示说明 |
第一次罗少飞行了 1 格,落在 2 号格子上,2 号格子的颜色是 2,所以跳跃到了下一个颜色是 2 的格子 5 号。 第二次罗少飞行了 3 格,落在 3 号格子上,3 号格子的颜色是 3,由于没有颜色等于 3 的下一个格子,所以无法跳跃。 第三次罗少飞行了 1 格,落在 4 号格子上,4 号格子的颜色是 1,所以跳跃到了下一个颜色是 1 的格子 1 号。 至此飞行完毕,终点是 1 号格子。 |
| 相关 |