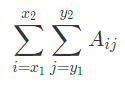4267:矩阵计数
时间限制:2 S / 内存限制:65536 KB
AC:8 / Submit:74
| 问题描述 |
|---|
罗少有一个 n * n 的矩阵 A,他想知道 A 矩阵中有多少个子矩阵满足,该子矩阵中所有元素之和是 K 的倍数。 形式化的,若我们用 (x1, y1) 和 (x2, y2) (保证 1 ≤ x1 ≤ x2 ≤ n,1 ≤ y1 ≤ y2 ≤ n)表示子矩阵的左下角和右上角,那么该子矩阵的和为:
你的目标是找到有多少对 (x1, y1) 和 (x2, y2) 满足该子矩阵的和是 K 的倍数,两种方案不同当且仅当 x1,y1,x2,y2 的任一数字不同。 |
| 输入描述 |
第一行是两个正整数 n 和 K 含义如描述。 接下来 n 行,每行 n 个整数表示 A 矩阵。 测试用例1:n ≤ 20,k ≤ 400 测试用例2:n ≤ 70,k ≤ 400 测试用例3:n ≤ 125,k ≤ 400 测试用例4:n ≤ 400,k ≤ 400 测试用例5:n ≤ 400,k ≤ 1e5 所有案例中,0 ≤ Aij < k。 |
| 输出描述 |
在一行中输出一个整数表示元素和是 K 的倍数的子矩阵的个数。 |
| 样例输入复制样例 |
3 3 1 2 1 2 1 2 1 2 1 |
| 样例输出 |
20 |
| 提示说明 |
放心大胆去暴力! |
| 相关 |