生成一棵随机树的算法
易向晚来适 2023-11-09
我们知道，树是由 n 个点，n - 1 条边构成的连通图，那么生成一棵随机的树，本人思考了这样一个算法：
从第 2 个点开始，每个点等概率的和前面 n - 1 个点进行连边，伪代码如下：
for (int i = 2; i <= nodeCount; i++)
{
int j = getRandomNumber(1, i - 1); // 等概率生成 1 ~ i-1 之间的随机数
link(i, j); // i j 连边
}
当然这种方法生成的树有可能会退化成一条链，但概率较小
为了避免这种情况，可以把 getRandomNumber 的第二个参数改成 i / 2，使这棵树变得紧凑
随机树生成后，可以在这个网站上看一下效果：https://csacademy.com/app/graph_editor/
测试图片（均为 20 个点）：
易向晚来适 2023-11-09
欢迎讨论这种做法的优劣，也可以交流一下如何生成一个 n 个点 m 条边的随机图？
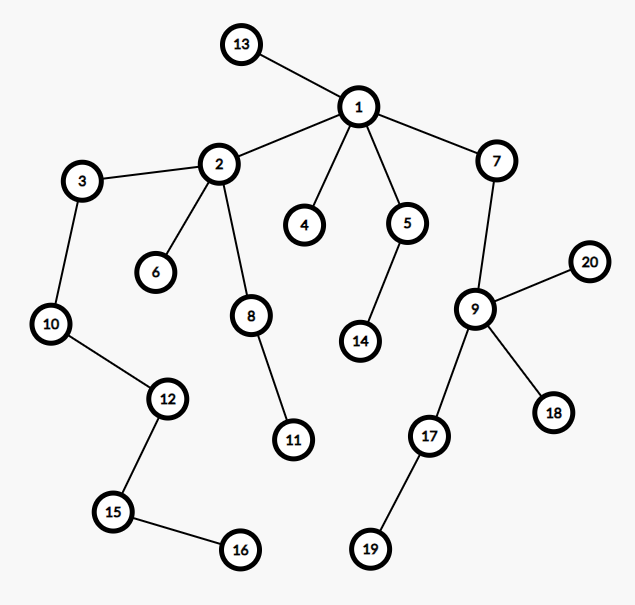
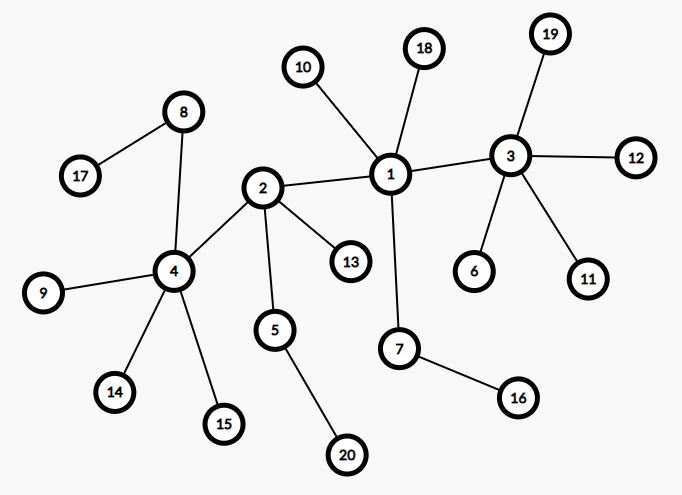
Silencer76 2023-11-10
也许可以这样，混合两种方式。
for (int i = 2; i <= nodeCount; i++)
{
int j,k=getRandomNumber(1,nodeCount)%10;
if(j<5) // 概率可以自己定，这里简单地设置为 二分之一
j = getRandomNumber(1, i - 1); // 等概率生成 1 ~ i-1 之间的随机数
else
j = getRandomNumber(1, i / 2); // 等概率生成 1 ~ i/2 之间的随机数
link(i, j); // i j 连边
}
Silencer76 2023-11-10
随手搓了一个生成代码，随机数+并查集。
``` c++
#include <iostream>
#include <fstream>
#include <random>
#include <ctime>
#include <algorithm>
using namespace std;
const int N=200100;
int pre[N]; // 上级数组
int Rank[N]; // 高度数组
void init(int n)
{ // 初始化
for(int i=0;i<=n;++i)
{
pre[i]=i; // 上级初始化为自己
Rank[i]=1; // 高度设置为 1
}
}
int find(int now)
{ // 查找函数
if(pre[now]==now) // 如果上级就是自己
return now; // 返回自己
else // 否则，向上查找，并且压缩路径
return pre[now]=find(pre[now]);
}
bool equal(int x,int y)
{ // 判断上级是否相等
return find(x)==find(y);
}
bool merge(int x,int y)
{ // 合并函数
x=find(x); // 查找 x 的上级
y=find(y); // 查找 y 的上级
if(x==y) // 如果上级一样
return false; // 不需要合并
else // 如果上级不一样
{ // 根据树的高度进行取舍
if(Rank[x]>Rank[y]) // 左子树高度大
pre[y]=x; // 所以 左子树的根 变成 右子树的根 的上级
else // 反之亦然
{ // 对于高度相同的，随意选择一边作为新上级
if(Rank[x]==Rank[y])
++Rank[y]; // 高度需要额外 +1
pre[x]=y; // 右子树的根 变成 左子树的根 的上级
}
return true;
}
}
int main(void)
{
ofstream in,out;
in.open("test1_in.txt");
out.open("test1_out.txt");
default_random_engine e;
uniform_int_distribution<int> u(1,998244353);
e.seed(time(0));
int n=100,i,x,y; // n 是节点个数
in<<n<<endl;
init(n);
for(i=1;i<n;++i) // 生成 n-1 条边
{
do{
x=u(e)%n+1; // 起点
y=u(e)%n+1; // 终点
}while(equal(x,y)); // 防止重边和自环
merge(x,y); // 表示已连接
in<<x<<' '<<y<<endl;
}
in.close();
out.close();
return 0;
} ```